正交切削中切屑温度分布的研究
发布日期:2011-11-25 兰生客服中心 浏览:2452
前言
 图1 正交连续成屑的切屑模型 |
1剪切面上的温度分布
 | (1) |
式中:a——散热系数
| q=0 x=0 0<y<8 | (2a) |
 y=tanfx | (2b) |
式中:r——材料密度
| limq=0 | (2c) |
 | (3) |
式中:

 图2 二维传热剪切面温度分布 |  图3 几何设定的影响 |
qe=qamh+(qA-qamh)exp(-py)
式中:qamh——室温
 | (3') |
式中:


2 切屑温度分布
 | (4) |
式中热参数R=rcvchhch/l,其相应的边界条件为
 | (5a) |
 | (5b) |
 | (5c) |
式中:Dqe——施于切屑的温度增量假定切屑上的热是均匀的,BC为平面热源。
 | (6) |
则有x=(hch-x)cosf/cosb对于(h,x)坐标系中qB显式,将式(6)代入式(3)得到细化的Weiner模型,代入式(3)得到作者提出的修正模型。
 | (7) |
 | (8) |
它满足热方程、边界条件以及式(5b)和式(5c )。如果满足式(5a)则要求式(5a)与式(8)完全相等,即
| qe(r,x)=qd | (9) |
 | (10) |
 (a)模型 |  (b)切屑温度分析 |
| 图4 切屑温度分布模型及切屑温度分布 | |
 | (11) |
 | (12) |
 | (13) |
将式(13)代入式(12),并用新参数g=lc/hch
 图5 切削温度分布 |  图6 刀—屑界面温度分布 |
3 结论
- 在以前的模型中假定工件一切屑自由表面为室温,而试验数据与之有较大差距;给出的模型比较切合实际。
- 为了简化计算,将切屑的流向近似为与剪切面相垂直,在实际切削中,分析剪切面温度分布是可行的。
- 在较高的切削速度下,沿剪切面向刀刃切削温度迅速达到稳定或饱和态,在这种情况下Rapier提出剪切面温度为常数的简化模型有一定的合理性。
- 直接测得的试验结果表明,采用作者提出的计算模型,可以得到金属切削温度分布较为满意的结果。
更多相关信息
-
空调压缩机阀板的加工工艺和精冲技术

一.引言 图1所示为某型空调压缩机剖视图,阀板是其中一项重要的功能件,它被广泛应用于轿车、磕碜人和货车等各种类型车辆、已经其他工业领域的制冷装置中。空调压缩机阀板大致有3种分类方法,按形状可分为圆形、方形和异性;按阀线可分为无阀线、单面阀
2016-07-19 -
浅谈汽车齿轮加工工艺发展动向

一、前言: 随着我国汽车制造业的发展,汽车齿轮加工行业也取得了长足的进步,汽车齿轮是汽车传动系统中极其重要的零部件,又是传动系统中的核心部件,所以说齿轮的品质直接关系到传动系统的品质,也是影响整车的性能和噪音的重要因素。因此,必须要更加深
2016-06-15 -
汽车覆盖件模具CAM工艺技术的研究
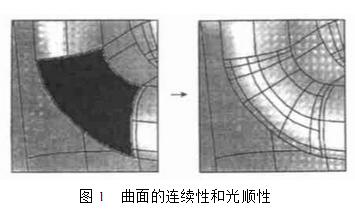
一、引言 在汽车制造中,汽车覆盖件与一般的机械产品从结构到制造工艺都有很大的区别,它具有曲面多、光顺性高、结构形状复杂、尺寸较大、精度要求高等特点,其模具制造技术难度大,成本高,开发周期和质量均难以控制。汽车大型覆盖件冲模CAD/CAE/
2016-06-15 -
浅谈加工数控机床本身大型结构件的工艺
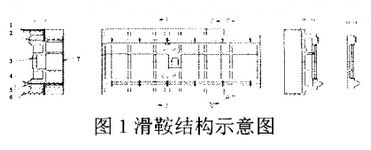
一、前言 作为机械制造业的母机,机床的设计制造水平一定程度上代表了一个国家的机械制造业水平。我国工业起步晚、基础较薄弱,造成中国当前的机床行业制造水平跟国际顶尖水平还存在一定的差距。机床的设计、部件制造、整体装配对机床的工作精度起着决定性
2016-04-29








